CAE e Design - Analisi Modale Ciclica Per Turbomacchine
- FGCAEANALYST

- 6 giorni fa
- Tempo di lettura: 6 min

L’analisi modale ciclica è una particolare analisi modale utilizzata su strutture che presentano una simmetria rispetto a un asse di rotazione, tale per cui la geometria e le proprietà strutturali si ripetono ciclicamente lungo i 360°.
Questa caratteristica consente di modellare solo una porzione della struttura, detta settore base, e di ricostruire il comportamento dinamico dell’intero sistema sfruttando le condizioni di periodicità.
Esempi tipici di strutture adatte a questo approccio sono:
ventilatori
turbine
giranti
ingranaggi
L’utilizzo dell’analisi modale ciclica permette:
una drastica riduzione del costo computazionale
una classificazione più completa dei modi di vibrazione
Terminologia
Vediamo la terminologia base per queste tipologie di simulazioni:
Settore Base: disegno geometrico scelto in modo che N ripetizioni in un sistema di coordinate cilindriche costituiscano la struttura completa;
Settore Angolare: viene indicato solitamente con a, ossia l'angolo coperto dal settore base, deve essere tale da restituire N x a = 360°. N è il numero di settori basi
Confini superiore e inferiore del settore base: le due facce del settore base che coprono il settore angolare e formano quindi i confini.

I Parametri Chiave
Nodal Diameter (ND)
Il Nodal Diameter rappresenta una linea diametrale lungo la quale lo spostamento è nullo durante la vibrazione di una struttura circolare ideale.
Fisicamente, il numero di diametri nodali indica quante onde di vibrazione sono presenti lungo la circonferenza:
ND = 1 → una sola onda
ND = 2 → due onde
ND = 3 → tre onde
Il nodal diameter fornisce la relazione che consente di ricostruire le forme modali dell’intera struttura a partire dall’analisi di un singolo settore. Le zone della struttura possono risultare in fase o in opposizione di fase, a seconda del valore di ND.

Harmonic Index (k)
Un altro parametro fondamentale è l’Harmonic Index, indicato con k. Si tratta di un numero intero che descrive la variazione di un singolo grado di libertà tra punti della struttura separati da un angolo pari al settore angolare.
Per un dato valore di k, lungo la circonferenza si manifesterà un certo numero di onde di vibrazione, direttamente correlate al numero di diametri nodali.
Relazione tra ND, k e m
Tra i parametri introdotti esiste una relazione fondamentale:
ND= k +- mN
dove:
k è l’harmonic index
N è il numero di settori
m è un parametro spaziale intero (0, 1, 2, …)
Il parametro m rappresenta l’ordine spaziale del modo e, al suo aumento, corrisponde generalmente un incremento della rigidezza dinamica e quindi della frequenza propria.
Va inoltre ricordato che:
se N è pari → kmax=N/2
se N è dispari → kmax=(N−1)/2
Collegamento con le frequenze di risonanza
La vera domanda è: come si collega tutto questo alle frequenze proprie della struttura?
Impostando il numero di settori, il valore di k ed il parametro spaziale m è possibile determinare tutti i possibili diametri nodali e, di conseguenza, calcolare un insieme completo di modi propri della struttura.
Caso m = 0
Con m = 0 si ottengono i modi fondamentali per ciascun valore di k.
Ad esempio, con un settore angolare di 90°:
k = 0 → nessuna onda viaggiante, l’intero disco vibra in fase
k = 1 → una linea nodale, due metà del disco in opposizione di fase
k = 2 → aumento delle zone in fase e in opposizione di fase
Aumento di m
Incrementando m, si accede a modi di ordine superiore, caratterizzati da frequenze più elevate e maggiore complessità spaziale della deformata.
Per ogni terna (ND, k, m) che soddisfa la relazione precedente, esiste una frequenza propria.
Perché l’analisi ciclica è superiore a quella completa
Rispetto all’analisi della struttura completa, l’analisi modale ciclica consente di:
Ridurre il costo computazionale: Si ottengono gli stessi modi e le stesse frequenze con un modello molto più leggero.
Classificare i modi dinamici. Infatti è possibile distinguere chiaramente:
modi in fase
modi degeneri
onde stazionarie
onde viaggianti
Un’onda viaggiante nasce dalla combinazione di due modi degeneri (identici per frequenza e forma, ma ruotati tra loro). Questa condizione è particolarmente critica perché può portare una stessa zona della struttura a essere continuamente sollecitata, con conseguente danneggiamento a fatica o risonanza.
Velocità dell’onda viaggiante
La velocità relativa dell’onda viaggiante si calcola come:
Vrel=fn/ND
dove:
fn è la frequenza propria (Hz)
ND è il numero di diametri nodali
Se la struttura ruota a questa velocità, il rischio di risonanza è reale.
CASO STUDIO: Analisi Modale Di Un Settore Circolare
Si consideri un settore circolare ottenuto a partire da una struttura completa a simmetria ciclica, come mostrato in figura. Il settore rappresenta una porzione della geometria totale che, ripetuta lungo l’asse di rotazione, ricostruisce l’intero componente.
L’obiettivo dell’analisi è:
calcolare le frequenze proprie di vibrazione del settore
confrontare i risultati ottenuti per Harmonic Index k = 0 e k = 1
verificare la corrispondenza con i primi modi propri della struttura completa

Modello e condizioni al contorno
Sul modello del settore sono state applicate:
condizioni di simmetria ciclica sulle due facce laterali
vincolo di incastro sulla parte inferiore della struttura
Queste condizioni permettono di riprodurre fedelmente il comportamento dinamico dell’intera struttura a partire da una porzione ridotta del modello.

Risultati
Considerando un harmonic index pari a 0, si ottiene il primo set di frequenze proprie del settore.
Analizzando il primo modo di vibrazione, si osserva chiaramente che si tratta di un modo torsionale del settore circolare.


Passando all’analisi modale della struttura completa, si ricerca il modo corrispondente alla stessa frequenza.
Il confronto mostra che:
il modo è effettivamente torsionale (dall'immagine si vede come la linea delle mesh ruoti), quindi fisicamente identico;
nella struttura completa, tuttavia, non è il primo modo, ma risulta essere il terzo modo proprio
Questo aspetto è fondamentale in quanto l’analisi ciclica individua correttamente il modo, ma lo svincola dall’ordine numerico imposto dalla presenza di altri modi globali.

Perché non analizzare direttamente la struttura completa?
Se il risultato è lo stesso, perché non risolvere sempre il modello completo?
La risposta è duplice:
Costo computazionale: a parità di risultato fisico, il modello ciclico richiede meno gradi di libertà e quindi il tempo di calcolo è significativamente inferiore, portando ad avere un consumo di risorse computazionali è ridotto. In altre parole: stesso risultato, meno effort.
Informazioni dinamiche più complete: l’analisi a simmetria ciclica consente qualcosa che l’analisi completa non offre in modo diretto, ossia la classificazione dei modi di vibrazione. In particolare è possibile distinguere modi in fase e modi con onda viaggiante, a seconda del numero di Harmonic Index considerati.
Analizziamo ora le velocità delle onde viaggianti per i casi di ND=0 e ND=1.
Caso ND = 0
Nel caso analizzato con ND = 0, la velocità dell’onda tende all’infinito. Non essendoci un’onda viaggiante, non si presentano criticità dinamiche associate a questa condizione, in quanto i modi sono principalmente modi di polmonazione.
Caso ND = 1
Considerando invece un modo con ND = 1 e frequenza fn≈680 Hz si ottiene una velocità dell’onda = 680 giri/s, pari a circa 40500 giri/min.
Se la struttura dovesse ruotare a una velocità prossima a questo valore, il rischio di risonanza diventerebbe concreto.
Si nota che il modo è lo stesso in quanto entrambi sono flessionali.


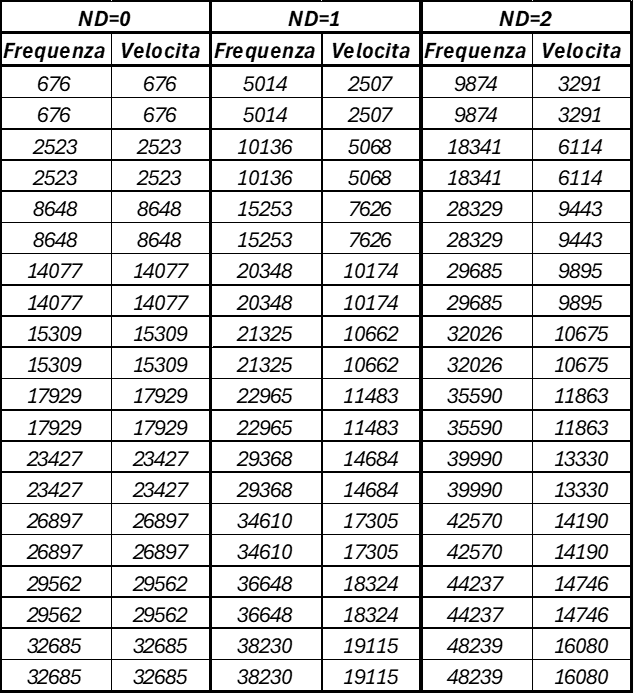
Analizzando le velocità dell'onda rispetto ai casi di Harmonic Index 1,2,3 e le relative frequenze, si vede che non sempre le frequenze più alte sono le più sicure. Infatti si nota come aumentando il numero di Diametri Nodali, la velocità di avanzamento dell'onda diminuisce, portando quindi ad una situazione in cui tale frequenza propria possa essere pari ad una velocità critica.

Considerazioni finali sul caso studio
Questo esempio mostra chiaramente come, considerando:
i diversi diametri nodali
le frequenze proprie associate
la natura del modo (stazionario o viaggiante)
sia possibile approfondire in modo significativo il comportamento dinamico della struttura senza ricorrere a complesse analisi di risposta in frequenza.
La conoscenza completa delle frequenze di risonanza in funzione del numero di diametri nodali consente inoltre di costruire strumenti fondamentali per l’analisi dinamica avanzata, quali:
diagramma di Campbell completo
diagramma a ventaglio
Questi argomenti saranno trattati nei prossimi articoli di CAE&Design.
---------------------------------------------------------------------------------------------------------------------------
FGCAEANALYST è al servizio delle aziende.
Hai un progetto che richiede un supporto alla progettazione?
Non aspettare: ogni giorno di ritardo costa tempo e risorse alla tua azienda.
Contattaci per una preventivo gratuito cliccando al seguente link.




Commenti