Tutta la componentistica progettata è sottoposta a fenomeni vibratori di diversa entità.
Ma possono questi fenomeni influire sulle prestazioni del sistema e portare magari alla rottura del componente?
Per poter rispondere a questa domanda, possiamo seguire diverse strade:
1) Effettuare un’analisi dinamica della struttura in esame andando a vedere come risponde al fenomeno eccitatorio (che può essere una forza esterna che viene applicata con andamento ciclico oppure del rumore bianco che viene applicato alle zone di vincolo)
2) Verificare se le vibrazioni della struttura e quella del carico sono paragonabili.
Come vediamo, le due modalità di approccio sono molto diverse. Ovviamente cambia anche la tipologia di output, nel senso che con il primo abbiamo la risposta della struttura a quella particolare tipologia di carico mentre con il secondo analizziamo una caratteristica intrinseca dell’oggetto da analizzare.
Data la complessità della prima scelta, che sicuramente risulta più completa ma ha anche tempistiche di esecuzione molto differenti, molto spesso basta solamente effettuare la seconda tipologia di analisi, cercando poi di interpretare i risultati.
Cosa significa pertanto verificare se le vibrazioni della struttura sono coincidenti con quelle del carico?
Ogni struttura, per il solo fatto di non essere rigida ma elastica, a seconda del modo con cui è vincolata nello spazio, tenderà a oscillare intorno ad una configurazione di equilibrio se sollecitata anche leggermente.
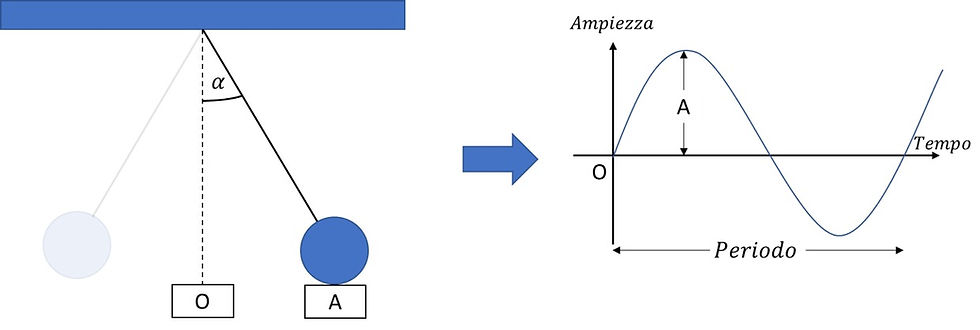
Figura 1: oscillazioni di un pendolo
Queste oscillazioni avranno un loro periodo (ossia un tempo in cui un punto passa per due volte nella stessa posizione) ed una loro ampiezza (ossia la distanza massima raggiunta da un punto rispetto al punto in equilibrio).
Queste due grandezze prendono il nome rispettivamente di frequenza propria e di modo proprio della struttura, ossia che “non dipendono dalla tipologia di carico, ma solamente dalla geometria e dal materiale” (non me ne vogliano gli esperti analisti dinamici per questa definizione molto grossolana).
Ovviamente stiamo parlando di condizioni in cui la struttura viene eccitata e poi lasciata vibrare senza forzante esterna.
Perché è importante conoscere queste grandezze?
La conoscenza di queste grandezze è fondamentale perché, conoscendo la frequenza di una struttura è possibile capire se essa entra o no in risonanza con una probabile forzante; nel caso le due frequente siano circa uguali, esse potrebbero portare all’insorgere del fenomeno della risonanza, ossia un aumento dell’energia del sistema e di conseguenza delle sue oscillazioni, portando pertanto al raggiungimento della deformazione a rottura con conseguente collasso della struttura stessa. (collasso che avviene ad un valore di forza al di sotto di quello per la struttura è progettata).
Il modo proprio di vibrare è importante conoscerlo in quanto fornirà informazioni su quali sono le zone che potrebbero essere soggette a deformazione massima (si pensi ad un pannello attaccato con quattro bulloni alle estremità che oscilla e in cui la parte centrale, oscillando, sbatta ripetutamente con un'altra struttura lì vicino).
Dal punto di vista puramente matematico, le frequenze proprie e i modi propri, non sono nient’altro che gli autovalori e gli autovettori di un sistema di equazioni.
Ma quale sistema?
Consideriamo il classico problema dinamico del sistema massa – molla di massa M e costante elastica K.
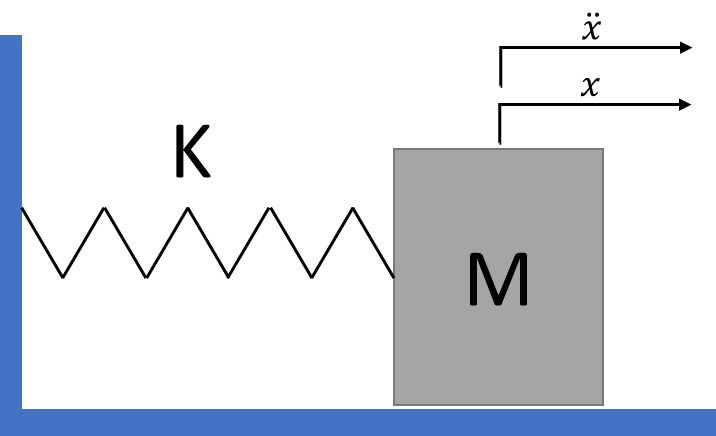
Figura 2: Sistema Massa - Molla non smorzato con rappresentata direzione di oscillazione.
L’equazione che si ottiene è la seguente:
Dove con x si intende lo spostamento mentre le grandezze con i punti sopra indicano le derivate rispetto al tempo.
Sostituendo alla x una soluzione sinusoidale, otteniamo:
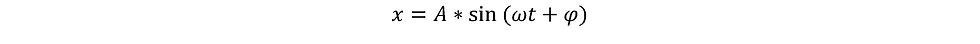
Derivando la grandezza rispetto al tempo due volte otteniamo pertanto:
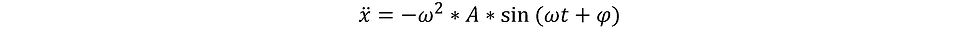
Sostituendo abbiamo:
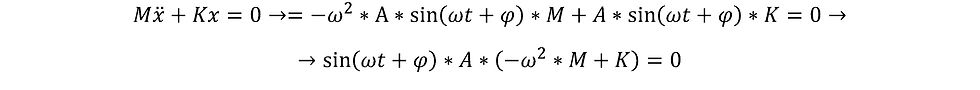
Questa equazione presenta due soluzioni, di cui la prima, ossia quella del termine al seno, non ci interessa.
Verificando la soluzione del secondo termine si ottiene:
Vediamo che la pulsazione del sistema dipende solamente dalla sua massa e dalla sua risposta elastica: più l’oggetto sarà rigido, maggiore sarà la sua frequenza, mentre maggiore è la massa, più lentamente vibrerà.
Estendendo questo problema ad una struttura complessa, come si trovano queste informazioni?
Analizziamo ad esempio un bracket come quello in figura.
Figura 3: Geometria della struttura analizzata
La struttura è vincolata per i fori, lo spessore della piastra 3 mm e il materiale è alluminio.
Essendo il sistema costituito da un numero molto elevato di gradi di libertà, il software, non impostando nessuna limitazione, andrà a calcolare tutti i modi propri possibile, pari proprio al numero di gradi di libertà della struttura. Perciò la ricerca sarà sempre limitata ad un numero finito di modi, in questo caso 5.
Ad analisi effettuata, abbiamo la seguente tabella delle frequenze:
Mentre le figure 4,5,6,7 e 8 riportano i primi 5 modi propri.
Figura 4: Primo modo proprio (4041 Hz)
Figura 5: Secondo modo proprio (4454 Hz)
Figura 6: Terzo modo proprio (4517 Hz)
Figura 7: Terzo modo proprio (5047 Hz)
Figura 8: Terzo modo proprio (5627 Hz)
Come sono stati ottenuti questi risultati?
Il primo passaggio, ripercorrendo quanto detto in precedenza, è quello di creare una mesh sulla geometria e di assegnare le proprietà di elementi e le caratteristiche di materiale (la densità è fondamentale in questa analisi).
Successivamente il software calcola le matrici di massa e di rigidezza e con queste informazioni risolve il sistema visto prima.
Infine, il software calcola i diversi parametri nodali relativi all’ampiezza della oscillazione, rapportando tutto alla dimensione massima e collezionando questi valori all’interno di un vettore. Tale vettore è proprio la deformata modale.
Come interpretare questi risultati?
Se la nostra struttura è sottoposta ad una forzante che ha come frequenza un valore circa simile a quelle in tabella, allora è necessario ridimensionare l’oggetto (aumentando o diminuendo la massa così da spostare le frequenze proprie al di fuori del range incriminato).
Inoltre la visualizzazione della deformata modale può aiutarci a capire se un modo è più o meno buono. Se ad esempio consideriamo si va a considerare un modello di trave a 6 elementi, l'ultimo modo (il 10 in questo caso) è rappresentato da diverse linee spezzate, il che significa che l'informazione che ci fornisce sul valore di frequenza non è veritiero. (figura 9).
Figura 9: Trave a 7 nodi. Il modo in questione è rappresentato da una spezzata, segno che il valore di frequenza non è veritiero.
Pertanto una buona regola di analisi è quella di avere almeno almeno 5 nodi nella semionda del modo in questione (figura 10).
Figura 10: Trave a 7 nodi. Il modo in questione ha almeno 5 nodi nella semionda di sinistra (rispetto i due nodi che fanno da perno).
Un uso alternativo che si può effettuare del calcolo modale tramite elementi finiti consiste nell’utilizzarlo per effettuare un check sul modello creato.
Se vogliamo verificare che tutti i vincoli siano inseriti correttamente, effettuando un analisi modale si andrà a verificare il modo di funzionamento del vincolo mentre invece se alcune parti sono libere di muoversi nello spazio, essere restituiranno una frequenza pari a 0 Hz, pertanto vasterà vedere quali sono queste zone e provvedere a contattarle con il resto della geometria.
Sempre tramite il solutore dell’analisi modale è possibile affrontare un altro problema, ossia l’analisi dei modi di buckling, meglio conosciuti come “problemi di instabilità” ma questo argomento sarà affrontato in un'altra #PilloleDiFem.
---------------------------------------------------------------------------------------------------------------------------
FGCAEANALYST è al servizio delle aziende. Ti seguiamo passo passo nell'analisi dei tuoi componenti mettendoci la stessa attenzione che metteremmo se fosse nostro.
Contattaci per una consulenza gratuita cliccando al seguente link.
Se invece vuoi imparare ad analizzare correttamente i tuoi progetti, contattami al seguente link.
Comments