CAE e Design - Il diagramma Di Campbell
- FGCAEANALYST

- 15 dic 2025
- Tempo di lettura: 5 min

Il Diagramma di Campbell è lo strumento principe per la progettazione nel mondo delle macchine rotanti (Turbine, Giranti, Ventilatori, compressori). Tale diagramma permette infatti di capire quando e come può avvenire la risonanza.
In questo articolo vediamo insieme cosa è di preciso e come si rappresenta.
Cos'è il diagramma di Campbell
Il diagramma di Campbell è un grafico che mette in relazione la velocità di rotazione del componente (RPM o rad/s) e le frequenze naturali della struttura.
Nel grafico vengono riportate:
Frequenze proprie della struttura: derivanti da analisi modale
Linee di eccitazione: 1× RPM, 2× RPM, ecc., che rappresentano le frequenze imposte dalla rotazione
I punti in cui le linee di eccitazione incrociano le frequenze proprie indicano velocità critiche, cioè regimi in cui la macchina può entrare in risonanza.
Fin qui è tutto molto semplice. Il fatto è che molti si fermano a calcolare le frequenze proprie nella condizione di zero carico, considerando le frequenze naturali costanti e invarianti rispetto alla velocità di rotazione.
Nella realtà le frequenze naturali dipendono dalla velocità di rotazione, anche se di poco, ed è per questo motivo che è fondamentale calcolare l'andamento modale per il range di funzionamento della macchina.
Si farà un esempio pratico prendendo ad esempio una girante e calcolando le frequenze proprie per la girante a diverse velocità di funzionamento.
CASO STUDIO: analisi modale di una girante
Si consideri la girante in figura. Il materiale è titanio. Si vuole studiare la risposta in frequenza nel range 0-10000 rad/s. La frequenza di funzionamento è di 2500 rad/s.

Di tale girante vengono analizzate le frequenze proprie nelle seguenti velocità di funzionamento tramite delle analisi modali prestressate:
0 rad/s
100 rad/s
1000 rad/s
10000 rad/s
Il risultato è la seguente tabella delle frequenze proprie di risonanza:

Riportando i dati su un grafico si ottiene il diagramma di Campbell per la struttura in questione:

Si può notare come tra 0 e 1000 rad/s le frequenze proprie rimangano costanti, mentre poi tendono ad aumentare con la velocità di rotazione.
Analizzando i valori di frequenza si nota come i modi sono simili a diversi gruppi.
In questo caso, ad esempio, il modo 2,3,4,5,6 hanno lo stesso valore di risonanza. Si riporta la deformata modale della struttura per il modo numero 2.

La vera domanda è: come si utilizza questo diagramma?
Per farlo si riportano le frequenze di funzionamento.
Solitamente queste sono la 1x (ossia pari alla velocità di rotazione), la 2x (ossia pari al doppio della velocità di rotazione). Inoltre per una turbina con un certo numero di palettature, esiste la Blade Passing Frequency, ossia la frequenza con cui una paletta rotorica incontra la paletta statorico.
Queste frequenze sono funzioni della velocità e sono rappresentate dalle seguenti equazioni:
1X -> f=w / 6.14
2X -> f=2*w / 6.14
BPF -> f = Z*w/ 6.14
Le velocità angolari w sono espresse in rad/s.
Sul grafico vado a riportare queste rette.
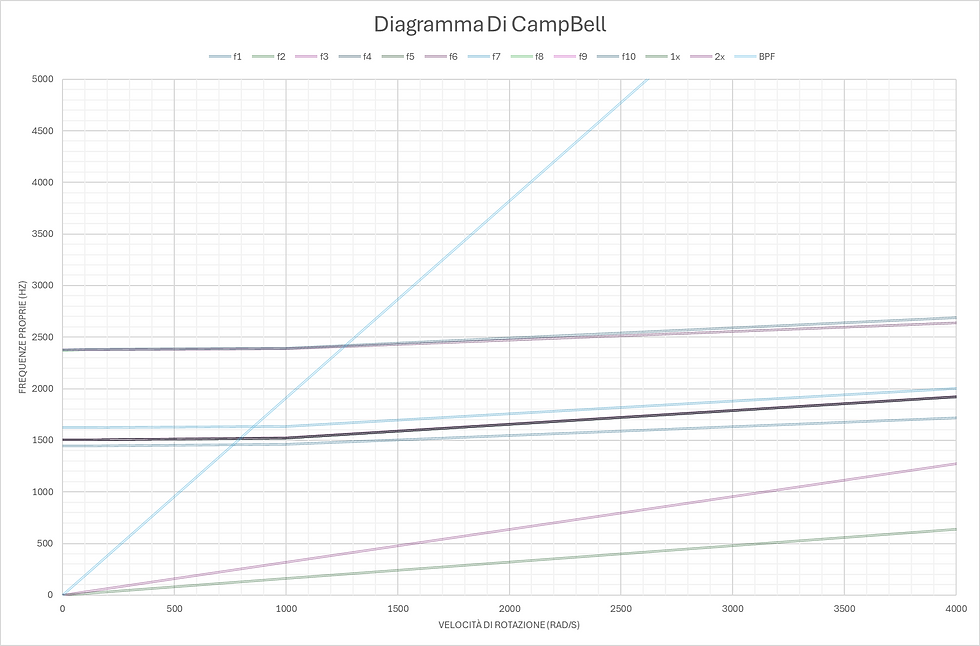

Guardando il grafico si vede l'eccitazione 1x e 2x non sono critiche, mentre è critica la Blade Passing Frequency.
Per tale valore di posso riscontrare 4 velocità di funzionamento critiche, ossia:
750 rad/s -> 7160 RPM
800 rad/s -> 7650 RPM
850 rad/s -> 8100 RPM
1250 rad/s -> 11900 RPM
Questo significa che la criticità non è causata da uno squilibrio ma da un eccitazione aerodinamica/periodica della palettatura, ossia non è causata da un rotore sbilanciato ma dall'aerodinamica.
Per procedere a un redesign consapevole è innanzitutto necessario stabilire se la risonanza intercetta il regime operativo continuo oppure se viene attraversata esclusivamente durante le fasi transitorie (avviamento e arresto). I due casi portano a scelte progettuali profondamente diverse.
Regime Continuo
Nel caso in cui la velocità di esercizio nominale ricada all’interno del range critico di una frequenza propria (tipicamente ±10%), la risonanza risulta persistente e non può essere tollerata. In questa condizione è necessario intervenire sul progetto, poiché il sistema lavorerebbe in risonanza per tempi prolungati.
Nel caso in esame, la velocità di funzionamento nominale è pari a circa 2500 rad/s. Dal diagramma di Campbell si osserva che a tale velocità la Blade Passing Frequency non intercetta alcuna frequenza propria significativa; pertanto, non si è in presenza di una criticità in regime continuo.
Avviamento
Se invece l’incrocio tra la BPF e una frequenza propria avviene esclusivamente durante le fasi di avviamento o arresto, la valutazione si sposta sulla velocità di attraversamento della zona critica.
Assumendo un intervallo critico pari a ±10% attorno alla pulsazione propria di circa 15000 rad/s, si ottiene un range complessivo di circa 2600 rad/s, considerando che le prime frequenze modali risultano tra loro molto ravvicinate.
Affinché l’attraversamento della risonanza non generi risposte dinamiche significative, il tempo di permanenza in tale intervallo deve essere molto inferiore al tempo caratteristico con cui un sistema smorzato sviluppa la risposta in risonanza. Tale tempo può essere stimato come:

dove i simboli sono da sinistra lo smorzamento strutturale e la pulsazione propria. Considerando uno smorzamento strutturale di 0.005 e una pulsazione propria di 15000 rad/s, si ottiene un tempo critico di 0.0133 s

Da questa stima è possibile ricavare il valore minimo dell’accelerazione di avviamento necessario affinché il sistema attraversi il range critico in un tempo sufficientemente breve, evitando l’amplificazione significativa delle vibrazioni.

Ne consegue che il sistema di avviamento deve essere progettato in modo da garantire una rampa di accelerazione almeno pari a tale valore, evitando soste o variazioni lente in prossimità della risonanza.
Le leve di progettazione
La gestione delle criticità individuate tramite il diagramma di Campbell può avvenire attraverso diverse leve progettuali, da selezionare in funzione del problema specifico:
Leva strutturale: Modifica delle rigidezze e delle masse per spostare le frequenze proprie.
Leva aerodinamica: Variazione del numero di palette, con conseguente spostamento della Blade Passing Frequency.
Leva di “sopravvivenza”: Incremento dello smorzamento strutturale per ridurre l’ampiezza della risposta in risonanza.
Leva di controllo: Gestione del transitorio di avviamento e arresto tramite opportune leggi di accelerazione.
Leva di accettazione: Accettazione consapevole della risonanza, limitata nel tempo e dimostrata tramite analisi quantitative.
Un ulteriore aspetto critico riguarda la completezza dell’analisi modale utilizzata per costruire il diagramma di Campbell. La domanda da porsi non è semplicemente quanti modi sono stati calcolati, ma piuttosto se i modi ottenuti siano realmente rappresentativi della dinamica del sistema.

L’analisi della percentuale di massa modale effettiva fornisce un’indicazione immediata in tal senso. Nel caso in esame si osserva come la descrizione dinamica risulti adeguata lungo l’asse di rotazione, mentre le modalità associate alle altre direzioni risultano praticamente non rappresentate. Questo indica che una parte significativa della dinamica del sistema non è stata catturata.
Di conseguenza, il diagramma di Campbell costruito a partire da tali risultati risulta intrinsecamente incompleto: alcune interazioni potenzialmente critiche tra eccitazioni e modi strutturali potrebbero non emergere semplicemente perché i modi corrispondenti non sono stati correttamente identificati.
Questo limite è tipico delle analisi modali “classiche” applicate a componenti assialsimmetrici, nelle quali non vengono intercettate tutte le modalità associate a fenomeni come:
degenerazione modale,
slittamento di fase delle onde viaggianti,
accoppiamenti non puramente assiali.
In questi casi è necessario ricorrere a analisi modali più avanzate, ad esempio introducendo formulazioni cicliche o modelli in grado di descrivere correttamente le famiglie modali complete, prima di poter considerare il diagramma di Campbell realmente affidabile ai fini progettuali.
Questi aspetti, spesso trascurati ma determinanti nella progettazione di componenti rotanti, saranno approfonditi in altri articoli dedicato della rubrica “CAE e DESIGN”, con esempi pratici e criteri operativi per valutare quando un’analisi modale può dirsi realmente completa.
---------------------------------------------------------------------------------------------------------------------------
FGCAEANALYST è al servizio delle aziende.
Hai un progetto che richiede un supporto alla progettazione?
Non aspettare: ogni giorno di ritardo costa tempo e risorse alla tua azienda.
Contattaci per una preventivo gratuito cliccando al seguente link.




Commenti