La maggior parte delle analisi FEM vengono effettuate in ambito lineare. Ma cosa significa precisamente?
Intorno al 1600 Robert Hooke scoprì una semplice relazione lineare tra la forza F e lo spostamento u, conosciuta come legge di Hooke.
dove K rappresenta la costante di rigidezza strutturale.
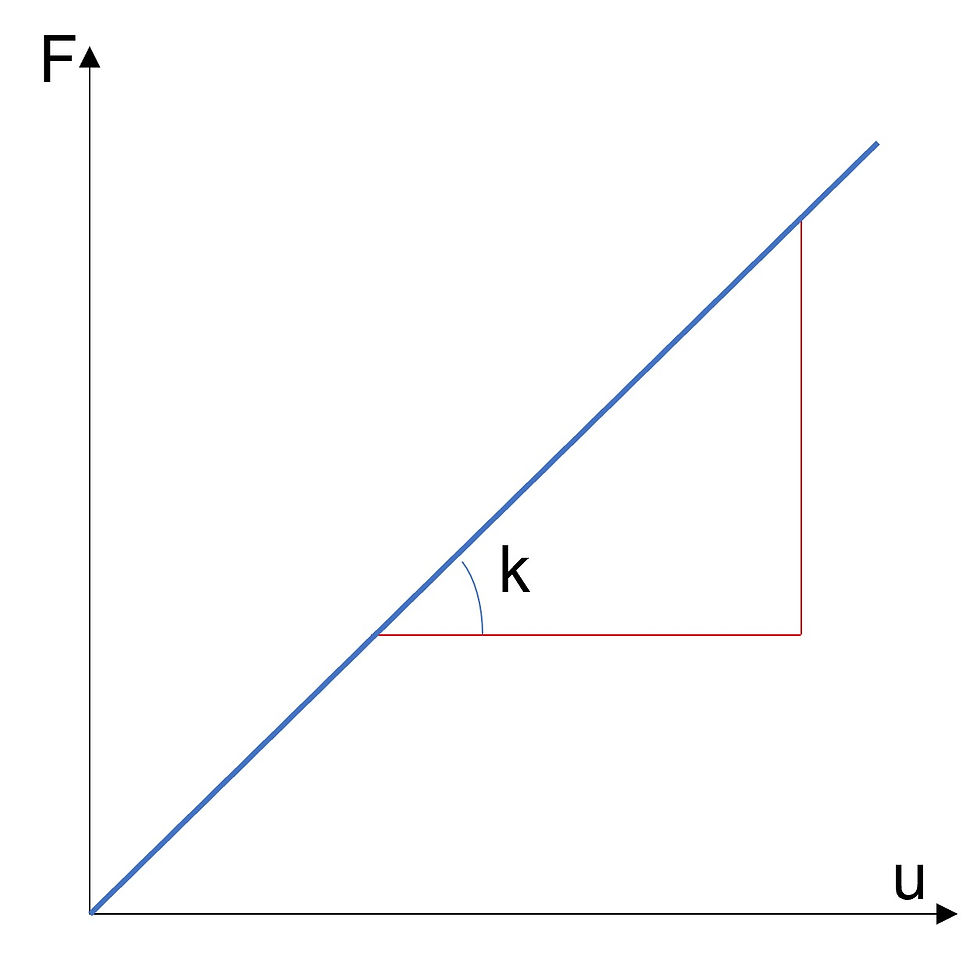
Figura 1: rappresentazione schematica della legge di Hooke
In questo caso si ha che la struttura è lineare in quanto obbedisce ad una legge di proporzionalità diretta.
Questo problema non presenta grandi complicazioni in quanto le strutture lineare sono ben rappresentate dalle analisi agli elementi finiti, in quanto sono basate sull’algebra lineare.
Ma vi sono un'enorme quantità di strutture che non obbediscono a questa tipologia di relazione tra forze e spostamenti. In questi casi la rigidezza non è più costante ma varia con il progredire del percorso di carico.
Figura 2: rappresentazione di un andamento non lineare di una legge elastica
Pertanto, possiamo affermare che una struttura è non lineare nel momento in cui il carico causa dei significativi cambiamenti nella rigidezza.
Possiamo raggruppare queste variazioni in tre grandi famiglie:
Quando le deformazioni superano il limite elastico del materiale (non linearità di materiale);
Se la struttura subisce grandi spostamenti, come una canna da pesca (non linearità di tipo geometrico);
Quando si ha una brusca variazione di stato, come ad esempio un contatto che si stacca sopra un certo limite oppure una parte che si rompe (non linearità di condizione al contorno).
N.B.: queste tre tipologie di non linearità si possono presentare insieme, non solamente isolate.
Come si risolvono questi problemi?
Poiché non siamo più nel campo lineare, la soluzione non può più essere predetta con un set di equazioni lineari (si dice che i termini al secondo ordine delle equazioni non sono più approssimabili). L’analisi numerica ci viene in aiuto, in quanto ci permette di poter utilizzare una serie iterativa di approssimazioni lineari del problema.
Uno dei metodi più utilizzati per risolvere questo tipo di problema è il metodo di Newton-Raphson. Per comprendere meglio il metodo consideriamo l’immagine in figura 3.
Di seguito una spiegazione del metodo senza troppi formalismi matematici:
Si calcola la rigidezza del sistema al punto 0, ipotizzando un comportamento lineare con costante elastica K0, la quale mi fornisce uno spostamento incrementale pari a du1.
Si calcola du1, si aggiorna lo spostamento totale aggiungendo l’incremento trovato allo spostamento del punto precedente (se è la prima iterazione allora quello del punto precedente sarà nullo) e successivamente si calcola la forza interna F1 del sistema corrispondente a questo spostamento.
Se la differenza tra la forza iniziale e la forza interna è sufficientemente piccola, allora si arresta il processo, altrimenti, conoscendo la rigidezza nella configurazione 2, si procede al calcolo di du2 applicando F* al sistema con k2 come rigidezza.
Si calcola il nuovo spostamento, si calcolano le forze interne del sistema nella configurazione di nuovo spostamento e si valuta la bontà del residuo rispetto al nuovo valore di forza calcolato, continuando con l’iterazione nel caso non sia soddisfatto tale requisito.
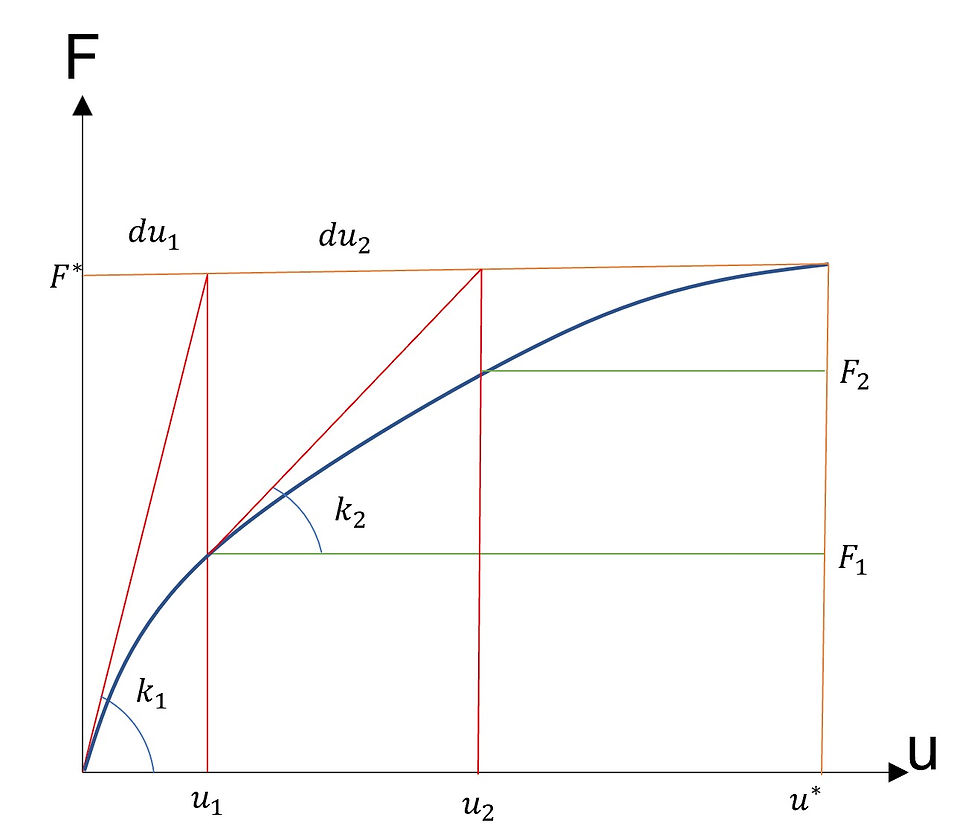
Figura 3: Schematizzazione del metodo di Newton-Raphson
Per comprendere meglio questo metodo consideriamo un materiale duttile che tende a incrudirsi con l’aumento del carico. Ipotizziamo pertanto di avere il carico costante ed i vincoli perfettamente rigidi. Come detto in precedenza, questo è un tipo di non linearità di materiale.
Per poter procedere nell’analisi il software agli elementi finiti ha necessità di avere una traccia su cui muoversi; pertanto, è necessario fornire al software la curva di incrudimento del materiale. Il modello più facile che si può fornire è il modello bilineare, rappresentato in figura 4
Figura 4: schematizzazione della curva stress-deformazione in modello bilineare.
In tale modello sono riportate due comportamenti, il comportamento lineare fino a snervamento (con costante elastica E) e successivamente si ipotizza un comportamento lineare dallo snervamento fino a rottura (con costante elastica pari a Et).
Come si può ben intuire questa tipologia di comportamento è un’ipotesi molto forte, ma il più delle volte, nelle comuni applicazioni è più che sufficiente per poter rappresentarne il comportamento. Con questo modello, il metodo di Newton-Rapson è in grado di calcolare le deformazioni e quindi gli spostamenti iterazione dopo iterazione, seguendo l’andamento della curva.
Ma come cambiano i risultati?
Per capire come cambiano i risultati con questo modello analizziamo la struttura in figura 5 sottoposta a due condizioni di carico:
1) Un caso in cui la forza è al di sotto del valore di snervamento (con F=78 N)
2) Un caso in cui la forza è superiore al valore limite (con F=7800 N)
Figura 5: geometria e schema di carico
La curva del materiale con modello bilineare è riportata in figura 6.
Figura 6: modello bilineare del materiale
Guardando i risultati, si nota come fintanto che si è al di sotto dei valori di snervamento i risultati non cambiano (figura 7).
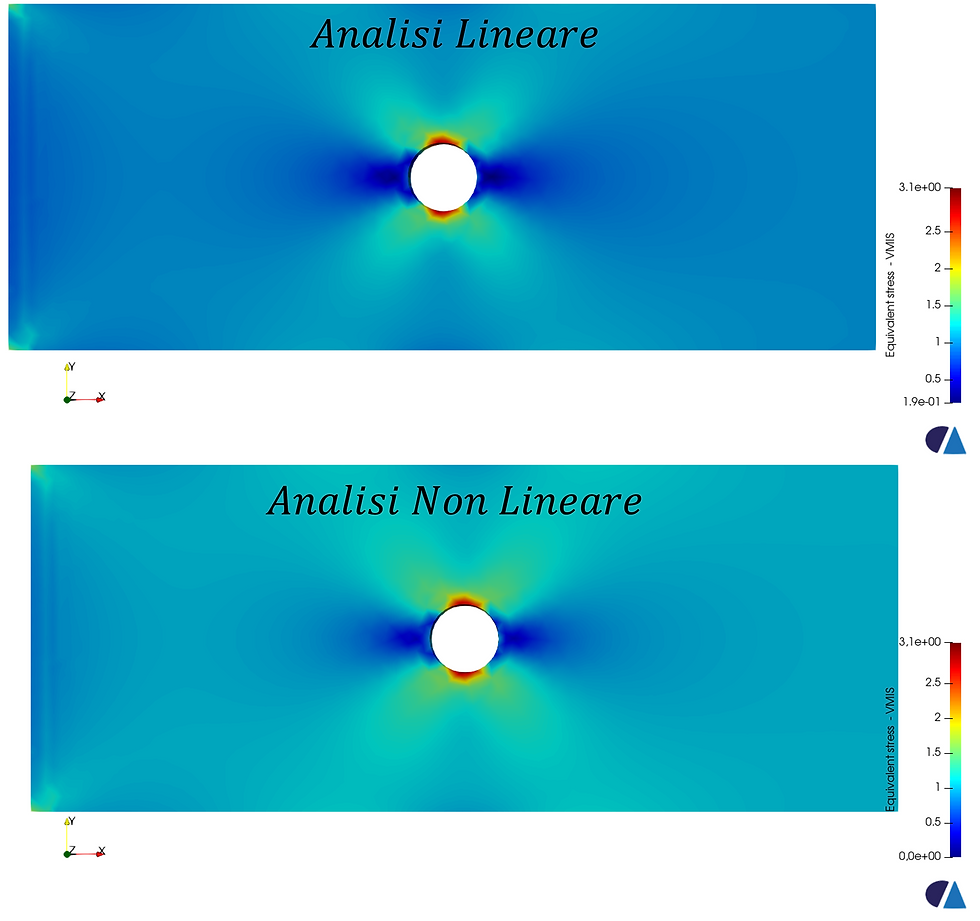
Figura 7: Confronto risposta della struttura nel caso di stress al di sotto del valore di snervamento
Quando invece il valore di stress supera il valore di snervamento (figura 8), nel caso di analisi lineare i valori di stress sono molto più elevati rispetto a quelli del modello bilineare. Infatti, superato il valore di snervamento, nel caso lineare il modello non aggiornerà la matrice di rigidezza con il nuovo valore di rigidezza, andando a commettere un errore sulla risposta della struttura, mentre nel caso non lineare, superato il valore di soglia di snervamento, il modello aggiornerà la matrice di rigidezza al nuovo valore, andando pertanto a determinare una nuova risposta.
Ovviamente viene da sé che il primo risultato non ha valenza fisica (dopo il valore di soglia la struttura non risponderà più in questo modo).
Infine, si si vuole avere un comportamento più prossimo a quello reale, il modello bilineare può essere sostituito con la curva reale di stress-strain ricavata da prova di laboratorio, definendola come funzione per punti, ovvero come piccole curve lineari.
Figura 8: Confronto risposta della struttura nel caso di stress al di sopra del valore di snervamento
Ma quando si deve utilizzare un modello non lineare per il materiale?
Tipicamente, a livello di progettazione, si deve progettare la struttura in comportamento lineare elastico prendendo come limite massimo il valore di snervamento, in quanto non si vuole che l’oggetto subisca dei cambiamenti di stato nella sua vita operativa (nessuno vuole una sedia che dopo il primo utilizzo a carico massimo si deformi permanentemente).
In alcuni casi però possono esserci carichi eccezionali previsti da normativa, in cui, a fronte dell’evento, l’oggetto deve essere comunque in grado di resistere anche quando si va in variazione di stato, prendiamo ad esempio un edificio durante un terremoto che subisce la formazione di cerniere plastiche, ossia la formazione di zone labili che prima non esistevano, e che introducono una possibilità di collasso o rottura della struttura.
Durante l'evento, anche se avviene tale fenomeno, la struttura deve comunque essere in grado di resistere per non ferire le persone che si trovano all'interno dell'abitazione.
Saranno poi i controlli eseguiti successivamente sull’oggetto che potranno dire se esso è ancora in grado di operare o se ha bisogno di manutenzione e/o sostituzione.
Un altro utilizzo molto usato dalle aziende consiste nell'utilizzare le analisi con non linearità del materiale per abbassare i valori massimi di stress e rientrare nei parametri di normativa previsti, per non dover ritornare indietro nella fase di progettazione del componente.
E le altre tipologie di non linearità?
Per quanto riguarda le altre tipologie di non linearità, esse saranno studio di altre #PILLOLEDIFEM.
---------------------------------------------------------------------------------------------------------------------------
FGCAEANALYST è al servizio delle aziende. Ti seguiamo passo passo nell'analisi dei tuoi componenti mettendoci la stessa attenzione che metteremmo se fosse nostro.
Contattaci per una consulenza gratuita cliccando al seguente link.
Se invece vuoi imparare ad analizzare correttamente i tuoi progetti, contattami al seguente link.
Bình luận